/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Urna

Zadanie nr 1920664

Dodaj do ulubionych
Dodaj do rozwiązanych

W pudełku znajdują się klocki o różnych kształtach i kolorach. Wiadomo, że prawdopodobieństwo wylosowania klocka, który ma kształt walca lub ma kolor czerwony jest równe 0,6. Prawdopodobieństwo, że losowo wybrany klocek czerwony jest walcem jest równe 0,25. Wiadomo też, że klocki czerwone stanowią 40% wszystkich klocków. Jakie jest prawdopodobieństwo, że losowo wybrany klocek w kształcie walca jest czerwony?

Rozwiązanie

Naszkicujmy diagram Venna.

PIC

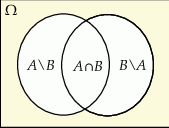
Jeżeli oznaczymy przez 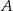A zdarzenie polegające na wyborze klocka czerwonego, a przez 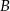B zdarzenie polegające na wyborze klocka w kształcie walca, to wiemy, że

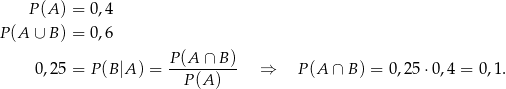
P (A) = 0,4 P (A ∪ B) = 0,6 P-(A-∩-B-) 0,25 = P(B |A ) = P (A ) ⇒ P (A ∩ B) = 0,25⋅ 0,4 = 0,1.

Stąd

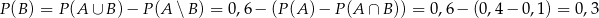
P(B ) = P(A ∪ B)− P(A ∖ B) = 0 ,6− (P (A) − P(A ∩ B)) = 0,6 − (0,4 − 0,1) = 0,3

i

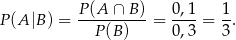
P(A ∩ B ) 0 ,1 1 P(A |B) = ----------= ---- = --. P(B ) 0 ,3 3

 
Odpowiedź: 13

Wersja PDF