/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Urna

Zadanie nr 2141633

Dodaj do ulubionych
Dodaj do rozwiązanych

Z pojemnika zawierającego 10 kul białych i 6 czarnych losujemy jedną kulę i wkładamy zamiast niej jedną kulę czarną. Oblicz prawdopodobieństwo tego, że jeżeli teraz wylosujemy z pojemnika dwie kule, to obie wylosowane kule będą białe.

Rozwiązanie

Mamy do czynienia z prawdopodobieństwem całkowitym – jeżeli najpierw wylosujemy kulę białą, to potem dwie kule losujemy spośród 9 białych i 7 czarnych, a jeśli najpierw wylosujemy kulę czarną, to potem dwie kule losujemy spośród 10 białych i 6 czarnych. Interesujące nas prawdopodobieństwo jest więc równe

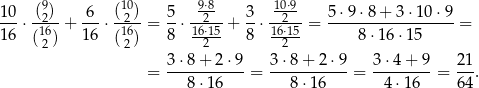
10 (9) 6 (10) 5 9⋅8 3 10⋅9- 5 ⋅9 ⋅8+ 3⋅1 0⋅9 ---⋅--2- + ---⋅ -2--= --⋅--2--+ --⋅--2--= ------------------= 16 (162) 1 6 (126) 8 16⋅215 8 16⋅215 8 ⋅16 ⋅15 3 ⋅8+ 2⋅9 3 ⋅8 + 2 ⋅9 3 ⋅4 + 9 21 = -----------= ----------- = -------- = --. 8⋅ 16 8 ⋅16 4⋅ 16 64

Możemy też tę sytuację przedstawić na drzewku.

PIC

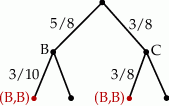
Rysując drzewko skorzystaliśmy z tego, że

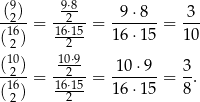
9 9⋅8 -(2)- -2--- -9⋅8--- -3- (16) = 16⋅15 = 16⋅1 5 = 1 0 2 2 (102) 102⋅9- 10 ⋅9 3 -16- = 16⋅15-= 16⋅1-5-= 8-. ( 2) 2

 
Odpowiedź: 2614

Wersja PDF