Zadanie nr 7370865
W urnie jest 7 kul czarnych i 3 białe. Losujemy z tej urny pięć razy po jednej kuli i po każdym losowaniu wkładamy wylosowaną kulę z powrotem do urny oraz dokładamy do urny dwie kule w kolorze wylosowanej kuli. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy wylosujemy kulę białą.
Rozwiązanie
Mamy do czynienia z prawdopodobieństwem całkowitym, które najlepiej byłoby zilustrować na drzewku, ale ze względu na dużą liczbę losowań (pięć) jest to mało praktyczne. Zamiast tego spróbujmy zastanowić się jak wyglądają zdarzenia sprzyjające. W każdym takim zdarzeniu mamy wylosowane 2 kule białe i 3 kule czarne. To oznacza, że dwa razy dokładamy 2 kule białe i trzy razy dokładamy po 2 kule czarne. Interesujące nas prawdopodobieństwo jest więc równe
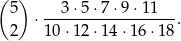
Symbol Newtona przed ułamkiem odpowiada wszystkim możliwym wyborom, w których losowaniach wybieramy białe kule (czyli jest to liczba sprzyjających ścieżek na drzewku). Natomiast ułamek to prawdopodobieństwo otrzymania dwóch białych kul, gdy już jest ustalone, w których losowaniach zostaną wybrane (czyli tak naprawdę, gdy ustalona jest droga na drzewku). Mianownik w tym ułamku odpowiada temu, że najpierw losujemy z 10 kul, potem z 12 itd. W liczniku: pierwszą z białych kul wybieramy spośród 3 kul, drugą spośród 5, pierwszą czarną spośród 7, drugą czarną spośród 9 i trzecią czarną spośród 11.
Pozostało obliczyć wartość powyższego wyrażenia.
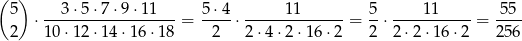
Odpowiedź: