Zadanie nr 7375624
W pierwszej urnie umieszczono 5 kul białych i 4 kule czarne, a w drugiej urnie 6 kul białych i 7 kul czarnych. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo wyjmujemy z drugiej urny jeszcze dwie kule koloru innego, niż kolor wylosowanej kuli. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą czarne.
Rozwiązanie
Szkicujemy drzewko, które opisuje wszystkie możliwe sytuacje w opisanym doświadczeniu.
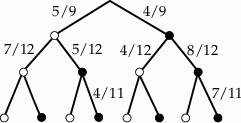
Zauważmy, że po wylosowaniu kuli z pierwszej urny, w drugiej urnie zawsze znajdzie się 12 kul – jeżeli z pierwszej wylosujemy białą kulę, to w drugiej będzie 7 kul białych i 5 czarnych, a jeżeli z pierwszej urny wylosujemy kulę czarną, to w drugiej będą 4 kule białe i 8 czarnych.
Ostatni wiersz w powyższym drzewku opisuje losowanie drugiej kuli z drugiej urny – podpisaliśmy tylko te prawdopodobieństwa, które są nam potrzebne, tzn. te odpowiadające zdarzeniom, gdy z drugiej urny wylosowaliśmy dwie kule czarne.
Interesujące nas prawdopodobieństwo jest więc równe
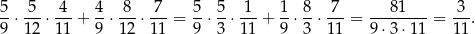
Odpowiedź: