/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Urna

Zadanie nr 9249684

Dodaj do ulubionych
Dodaj do rozwiązanych

W każdej z dwóch szuflad jest tyle samo rękawiczek prawych i lewych, a trzecia szuflada jest pusta. Z każdej z dwóch pierwszych szuflad losujemy jedną rękawiczkę i wkładamy je do trzeciej szuflady. Następnie z trzeciej szuflady losujemy jedną rękawiczkę. Oblicz prawdopodobieństwo tego, że rękawiczka wylosowana z trzeciej szuflady jest lewa.

Rozwiązanie

Sposób I

Zauważmy, że rękawiczki lewe i prawe pełnią w tym zadaniu dokładnie taką samą rolę (jest ich dokładnie tyle samo), więc prawdopodobieństwo wybrania z trzeciej szuflady rękawiczki lewej musi być takie samo, jak prawdopodobieństwo wybrana z niej rękawiczki prawej. Ponieważ te dwa zdarzenia są rozłączne i wzajemnie przeciwne, prawdopodobieństwo każdego z nich musi być równe 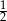1 2 .

Sposób II

Jeżeli myślimy o przebiegu opisanego doświadczenia, to po losowaniu z dwóch pierwszych szuflad mamy cztery (jednakowo prawdopodobne) możliwe sytuacje: 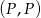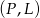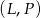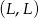(P,P ) , (P,L ) , (L,P ) , (L,L ) . W pierwszej sytuacji nie ma możliwości wylosowania rękawiczki lewej z trzeciej szuflady, w dwóch kolejnych prawdopodobieństwo wylosowania rękawiczki lewej jest równe 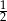1 2 , a w czwartej prawdopodobieństwo to jest równe 1. Ze wzoru na prawdopodobieństwo całkowite interesujące nas prawdopodobieństwo jest więc równe

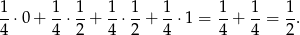
1⋅ 0+ 1-⋅ 1-+ 1-⋅ 1+ 1-⋅1 = 1-+ 1-= 1. 4 4 2 4 2 4 4 4 2

Możemy też tę sytuację przedstawić na drzewku.

PIC

 
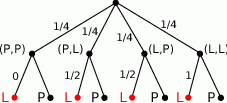
Odpowiedź: 1 2

Wersja PDF