/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 1938357

W stożku o promieniu podstawy r tworząca jest nachylona do płaszczyzny podstawy pod kątem α . Przez wierzchołek stożka poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem β > α .

PIC

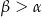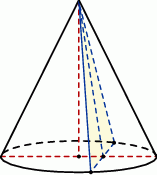
Wykaż, że pole otrzymanego przekroju stożka jest równe

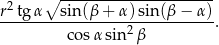
2 ∘ ---------------------- r-tg-α--sin(β-+-α-)sin(β-−-α)-. cos αsin2 β
Wersja PDF

Rozwiązanie

Zaznaczmy podane kąty nachylenia.

PIC

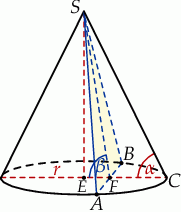
Obliczmy najpierw długości wysokości i tworzącej stożka. Patrzymy na trójkąt prostokątny 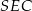SEC .

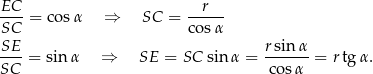
EC--= cos α ⇒ SC = --r-- SC co sα SE rsin α --- = sin α ⇒ SE = SC sin α = ------ = r tg α. SC co sα

Otrzymany przekrój to trójkąt równoramienny 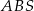ABS o podstawie 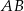AB i wysokości 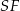SF . Długość wysokości obliczamy bez trudu z trójkąta prostokątnego SEF .

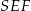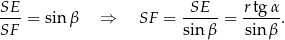
SE SE rtg α --- = sin β ⇒ SF = -----= -----. SF sin β sinβ

Aby obliczyć długość podstawy trójkąta 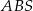ABS patrzymy na trójkąt prostokątny AF S .

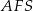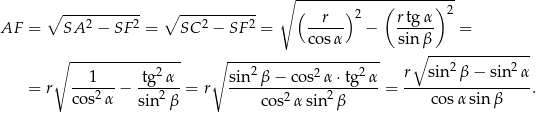
∘ ---------------------- ∘ ----------- ∘ ----------- ( r )2 ( rtgα ) 2 AF = SA 2 − SF2 = SC 2 − SF2 = ----- − ----- = co sα sin∘β--------------- ∘ ---------------- ∘ --------------------- 2 2 --1--- -tg-2α- sin-2β-−-cos2-α⋅-tg-2α- r--sin-β-−--sin--α- = r cos2 α − sin2β = r cos2 αsin2β = co sα sin β .

Pole interesującego nas przekroju jest więc równe

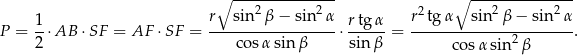
∘ --------------- ∘ --------------- r sin2β − sin2 α r2 tgα sin 2β − sin2 α P = 1⋅AB ⋅SF = AF ⋅SF = ------------------⋅ rtg-α =-----------------------. 2 co sα sin β sinβ cos αsin2 β

Otrzymany wzór to prawie wzór, który mieliśmy udowodnić. Pozostało wykazać, że

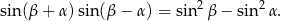
2 2 sin (β + α)sin(β − α ) = sin β − sin α.

Zrobimy to na dwa sposoby.

Sposób I

Przekształcamy lewą stronę korzystając ze wzorów na sinus sumy/różnicy.

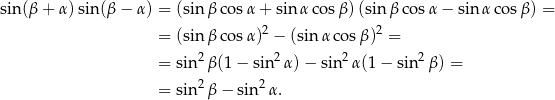
sin (β + α) sin (β − α) = (sinβ cos α+ sin α cosβ )(sinβ cos α− sin α cos� = (sinβ cos α)2 − (sin α cosβ )2 = 2 2 2 2 = sin β (1− sin α) − sin α (1− sin β) = = sin2β − sin2 α.

Sposób II

Przekształcamy prawą stronę korzystając ze wzorów na sumę/różnicę sinusów oraz ze wzoru na 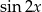sin 2x .

2 2 sin β − sin α = (sinβ − sin α)(sinβ + sin α) = β-−-α- β-+-α- β-+-α- β-−-α- = 2 sin 2 cos 2 ⋅2 sin 2 co s 2 = ( β − α β − α) ( β + α β + α ) = 2sin ------cos ------ 2 sin ------co s------ = 2 2 2 2 = sin(β − α) sin (β+ α).
Wersja PDF