Zadanie nr 2291671

Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy 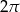2 π . Oblicz kąt rozwarcia stożka.

Rozwiązanie

Rozpoczynamy od rysunku – oznaczmy kąt rozwarcia kąta przez .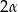

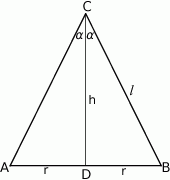
Sposób I

Zapiszmy podaną informację o stosunku pól.

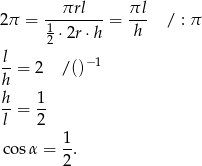
2π = ---πrl-- = πl- / : π 12 ⋅2r ⋅h h l --= 2 / ()−1 h h- 1- l = 2 1 cosα = -. 2

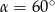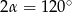Zatem α = 6 0∘ i kąt rozwarcia stożka jest równy 2α = 120∘ .

Sposób II

Zauważmy, że

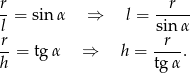
r = sin α ⇒ l = --r-- l sin α r-= tg α ⇒ h = -r--. h tgα

Zapiszmy podaną informację o stosunku pól.

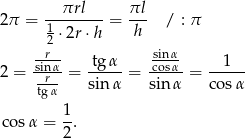
---πrl-- πl- 2π = 1⋅2r ⋅h = h / : π 2 srinα- -tg-α- -scinosαα --1-- 2 = -r- = sin α = sin α = cosα tgα 1- c osα = 2.

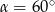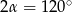Zatem α = 6 0∘ i kąt rozwarcia stożka jest równy 2α = 120∘ .

Sposób III

Zapiszmy podaną informację o stosunku pól (korzystamy ze wzoru na pole trójkąta z sinusem).

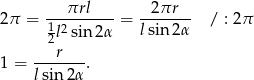
2π = ---πrl----= -2πr--- / : 2 π 1l2sin 2α lsin 2α 2r 1 = -------. lsin 2α

Zauważmy, że ponadto

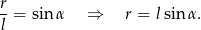
r l = sin α ⇒ r = lsin α.

Mamy zatem

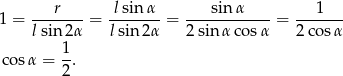
1 = ---r--- = -lsinα- = ---sin-α----= ---1--- lsin2 α l sin 2α 2sin αco sα 2c osα 1 cosα = -. 2

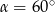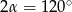Zatem α = 6 0∘ i kąt rozwarcia stożka jest równy 2α = 120∘ .
Odpowiedź: ∘ 120