Zadanie nr 2558194
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 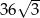 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 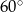 . Oblicz objętość stożka.
. Oblicz objętość stożka.
Rozwiązanie
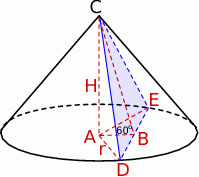
Zacznijmy od rysunku i oznaczmy przez 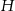 i
i  wysokość i promień podstawy stożka oraz przez
wysokość i promień podstawy stożka oraz przez  długość boku trójkąta równobocznego w przekroju.
długość boku trójkąta równobocznego w przekroju.
Z podanego pola przekroju mamy
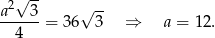
Plan jest następujący: z trójkąta 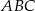 wyliczymy długość wysokości, a z trójkąta prostokątnego
wyliczymy długość wysokości, a z trójkąta prostokątnego 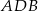 długość promienia podstawy.
długość promienia podstawy.
Liczymy
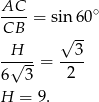
Podobnie
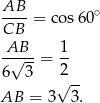
Stosujemy teraz twierdzenie Pitagorasa w trójkącie 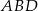 .
.
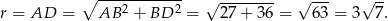
Stąd szukana objętość
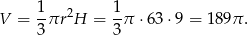
Odpowiedź: