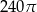Zadanie nr 2658696
Cosinus kąta rozwarcia stożka jest równy 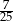 . Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
. Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
Rozwiązanie
Rysujemy przekrój osiowy opisanej sytuacji.
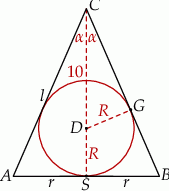
Oznaczmy przez  promień podstawy stożka,
promień podstawy stożka, 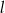 długość jego tworzącej,
długość jego tworzącej, 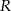 promień kuli wpisanej,
promień kuli wpisanej, 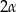 – kąt rozwarcia stożka. Widać, że z trójkąta
– kąt rozwarcia stożka. Widać, że z trójkąta 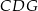 łatwo obliczyć
łatwo obliczyć 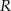 , ale zanim to zrobimy musimy obliczyć funkcje trygonometryczne kąta
, ale zanim to zrobimy musimy obliczyć funkcje trygonometryczne kąta  . Korzystamy ze wzoru
. Korzystamy ze wzoru
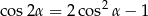
Mamy zatem
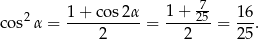
Kąt  jest ostry, więc
jest ostry, więc 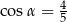 i
i
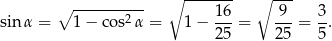
Patrzymy teraz na trójkąt prostokątny 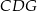 .
.
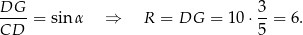
Teraz patrzymy na trójkąt 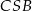
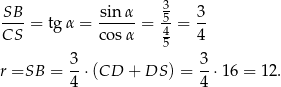
Stąd
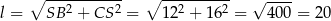
i pole powierzchni bocznej jest równe
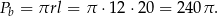
Odpowiedź: