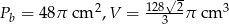/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 3230740

Dodaj do ulubionych
Dodaj do rozwiązanych

Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 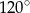12 0∘ . Wiedząc, że tworząca stożka ma długość 12 cm, oblicz pole powierzchni bocznej i objętość tego stożka.

Rozwiązanie

Zaczynamy od rysunku.

PIC

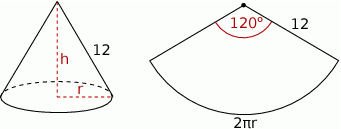
Pole powierzchni bocznej jest wycinkiem koła o promieniu równym tworzącej stożka. Zatem długość wycinka koła jaki tworzy wynosi

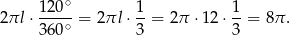
∘ 2πl ⋅ 120--= 2 πl ⋅ 1-= 2π ⋅12⋅ 1-= 8 π. 360∘ 3 3

Stąd otrzymujemy równanie

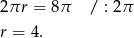
2πr = 8π / : 2π r = 4.

Teraz możemy obliczyć pole powierzchni bocznej

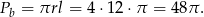
P = πrl = 4 ⋅12⋅ π = 4 8π. b

Z twierdzenia Pitagorasa obliczamy wysokość stożka

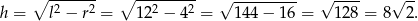
∘ ------- ∘ --------- 2 2 2 2 √ --------- √ ---- √ -- h = l − r = 12 − 4 = 14 4− 16 = 128 = 8 2.

Teraz obliczamy objętość

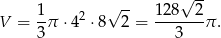
√ -- √ -- V = 1π ⋅ 42 ⋅8 2 = 128---2π . 3 3

 
Odpowiedź: √- Pb = 4 8π cm 2,V = 1283-2π cm 3

Wersja PDF