/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 3942306

Pole powierzchni całkowitej 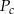Pc stożka oraz jego pole podstawy 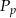Pp spełniają równanie 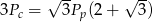√ -- √ -- 3Pc = 3Pp (2+ 3) . Oblicz miarę kąta rozwarcia stożka.

Wersja PDF

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

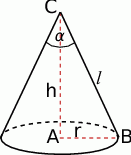
Podstawmy

2 Pc = πrl + πr P = πr 2 p

do danego równania.

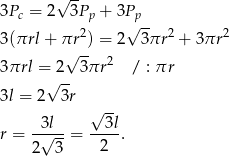
3P = 2√ 3P + 3P c p √ p- 3(πrl + πr2) = 2 3 πr2 + 3πr 2 √ -- 2 3πrl = 2 3πr / : πr √ -- 3l = 2 3r √ -- 3l 3l r = -√---= ----. 2 3 2

Patrzymy teraz na trójkąt 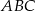ABC .

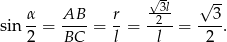
√3l √ -- sin α-= AB--= r = --2- = --3. 2 BC l l 2

Zatem 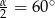α2 = 60∘ , czyli α = 120∘ .  
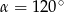Odpowiedź: α = 120∘

Wersja PDF