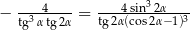Zadanie nr 4476910
Tworzącą stożka widać ze środka kuli wpisanej w ten stożek pod kątem o mierze  . Wyznacz stosunek objętości tej kuli do objętości stożka.
. Wyznacz stosunek objętości tej kuli do objętości stożka.
Rozwiązanie
Zaczynamy oczywiście od rysunku – od razu rysujemy przekrój osiowy opisanej sytuacji.
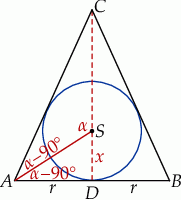
Zauważmy najpierw, że w trójkącie prostokątnym 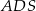
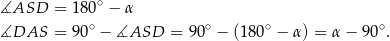
Dodatkowo, odcinek 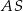 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 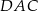 , więc
, więc
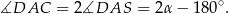
Teraz łatwo już obliczyć wysokość stożka w zależności np. od promienia  jego podstawy.
jego podstawy.
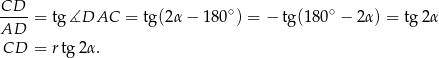
Objętość stożka jest więc równa
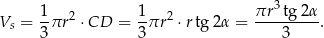
Objętość kuli wpisanej w stożek obliczymy na dwa sposoby.
Sposób I
Jeżeli oznaczymy przez  promień kuli wpisanej w stożek, to w trójkącie
promień kuli wpisanej w stożek, to w trójkącie  mamy
mamy
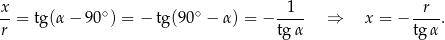
Objętość kuli wpisanej w stożek jest więc równa
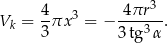
W takim razie stosunek objętości kuli do objętości stożka jest równy
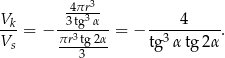
Sposób II
Standardowy sposób wyznaczenia promienia  okręgu wpisanego w trójkąt to wzór na pole
okręgu wpisanego w trójkąt to wzór na pole 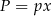 , gdzie
, gdzie 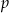 jest połową obwodu tego trójkąta. W naszej sytuacji
jest połową obwodu tego trójkąta. W naszej sytuacji
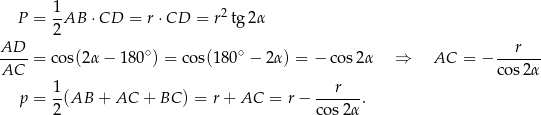
Promień kuli wpisanej w stożek jest więc równy
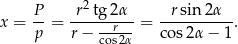
Interesujący nas stosunek objętości jest więc równy
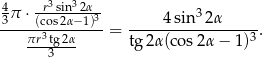
No i mamy dobre ćwiczenie, żeby sprawdzić, że jest to ten sam wynik co poprzednio.
Odpowiedź: