Zadanie nr 4847429
Dwie kule mające średnice 4 cm i 1 cm wpisano w stożek w ten sposób, że większa jest styczna do podstawy i powierzchni bocznej stożka, zaś mniejsza – do powierzchni bocznej stożka i do większej kuli. Oblicz pole powierzchni tego stożka.
Rozwiązanie
Rysujemy przekrój osiowy opisanej sytuacji.
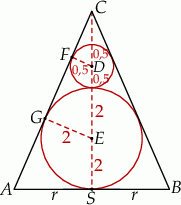
Oznaczmy przez 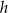 wysokość, a przez
wysokość, a przez  promień podstawy stożka. Z podobieństwa trójkątów
promień podstawy stożka. Z podobieństwa trójkątów 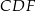 i
i 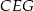 możemy obliczyć
możemy obliczyć 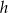 .
.
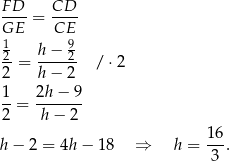
Promień podstawy i tworzącą stożka możemy obliczyć np. z podobieństwa trójkątów  i
i 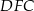 , ale zanim to zrobimy, obliczmy długość odcinka
, ale zanim to zrobimy, obliczmy długość odcinka 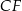 .
.
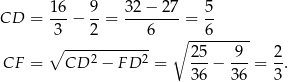
Teraz korzystamy z podobieństwa trójkątów 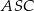 i
i 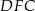 .
.
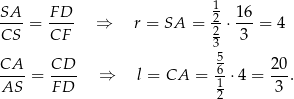
Pozostało obliczyć pole powierzchni stożka.
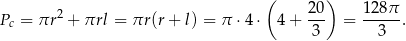
Odpowiedź: