/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 5888468

Dodaj do ulubionych
Dodaj do rozwiązanych

Objętość stożka, w którym wysokość jest równa promieniowi podstawy, jest równa 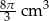8π3-cm 3 . Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie 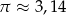π ≈ 3,1 4 podaj wynik z dokładnością do 0,1.

Rozwiązanie

Narysujmy przekrój osiowy stożka.

PIC

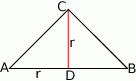
Ze wzoru na objętość stożka mamy równość

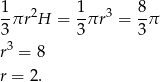
1-πr2H = 1πr 3 = 8π 3 3 3 r3 = 8 r = 2.

Aby obliczyć pole powierzchni bocznej musimy jeszcze znać długość tworzącej 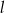l . Obliczamy ją z trójkąta prostokątnego ADC .

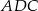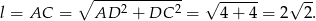
∘ ------------ √ ------ √ -- l = AC = AD 2 + DC 2 = 4 + 4 = 2 2.

Stąd

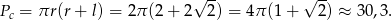
√ -- √ -- Pc = πr (r+ l) = 2π(2 + 2 2) = 4π (1+ 2) ≈ 30,3.

 
Odpowiedź: 30,3 cm 2

Wersja PDF