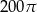/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 5957913

W stożek o wysokości 10 wpisano kulę o promieniu 4. Oblicz pole powierzchni całkowitej stożka.

PIC

Wersja PDF

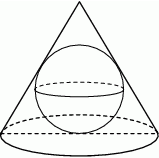
Rozwiązanie

Dorysujmy wysokość stożka oraz promień kuli wpisanej.

PIC

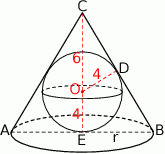
Zauważmy, że 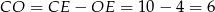CO = CE − OE = 10 − 4 = 6 oraz

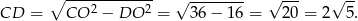
∘ ------------ √ -------- √ --- √ -- CD = CO 2 − DO 2 = 3 6− 16 = 20 = 2 5.

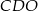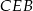Zauważmy ponadto, że trójkąty CDO i CEB są podobne (bo oba są prostokątne i mają wspólny kąt 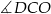∡DCO ). Korzystając z tego podobieństwa mamy

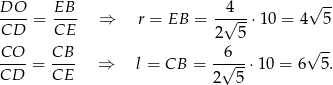
DO-- EB-- -4--- √ -- CD = CE ⇒ r = EB = 2√ 5-⋅10 = 4 5 √ -- CO-- = CB-- ⇒ l = CB = -√6--⋅ 10 = 6 5. CD CE 2 5

Pole powierzchni całkowitej jest więc równe

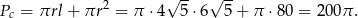
√ -- √ -- Pc = πrl + πr 2 = π ⋅4 5 ⋅6 5 + π ⋅80 = 200π .

 
Odpowiedź: 200 π

Wersja PDF