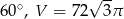/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 6015402

Dodaj do ulubionych
Dodaj do rozwiązanych

Połówkę koła o promieniu 12 zwinięto w stożek. Oblicz objętość i kąt rozwarcia tego stożka jeżeli długość łuku tej połówki koła jest obwodem podstawy, a jej promień jest tworzącą stożka.

Rozwiązanie

Najtrudniejsze w tym zadaniu to wyobrazić sobie o co chodzi. Najłatwiej chyba myśleć od końca: jeżeli rozetniemy stożek wzdłuż tworzącej to dostajemy wycinek kołowy. Tu robimy na odwrót, zaczynamy od wycinka koła (który akurat jest połówką koła) i sklejamy z tego stożek.

PIC

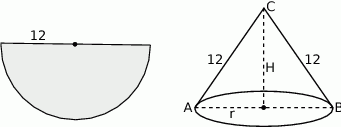
Obliczmy promień podstawy stożka. Wiemy, że długość okręgu w podstawie jest równa łukowi półkola, czyli wynosi

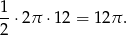
1-⋅2 π ⋅12 = 12 π. 2

Z drugiej strony jest ona równa 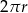2πr . Stąd 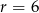r = 6 . Zatem 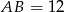AB = 12 i trójkąt 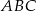ABC jest równoboczny, czyli kąt rozwarcia stożka wynosi 60 ∘ .

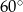Wysokość stożka możemy łatwo wyliczyć ze wzoru na wysokość w trójkącie równobocznym.

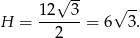
√ -- √ -- H = 12--3-= 6 3. 2

Zatem jego objętość jest równa

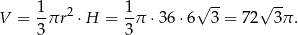
1 1 √ -- √ -- V = -πr 2 ⋅H = -π ⋅36 ⋅6 3 = 72 3π . 3 3

 
Odpowiedź: √ -- 60∘, V = 72 3π

Wersja PDF