Zadanie nr 6445316
Wysokość stożka podzielono na trzy równe odcinki i przez punkty podziału poprowadzono płaszczyzny równoległe do podstawy. Oblicz stosunek objętości powstałych brył.
Rozwiązanie
Narysujmy przekrój osiowy opisanej sytuacji.
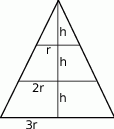
Jeżeli przez  i
i 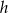 oznaczymy promień podstawy i wysokość w najmniejszym stożku, to na mocy twierdzenia Talesa, kolejne stożki mają promienie i wysokości odpowiednio
oznaczymy promień podstawy i wysokość w najmniejszym stożku, to na mocy twierdzenia Talesa, kolejne stożki mają promienie i wysokości odpowiednio 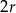 i
i 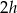 oraz
oraz 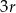 i
i 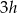 . Objętości tych trzech stożków wynoszą zatem
. Objętości tych trzech stożków wynoszą zatem
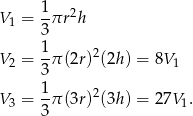
Stąd objętości otrzymanych brył (ściętych stożków), to
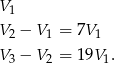
Szukane stosunki to 19:7:1.
Odpowiedź: 19:7:1

