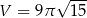/Szkoła średnia/Geometria/Stereometria/Stożek

Zadanie nr 9363780

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka

Rozwiązanie

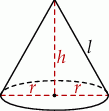
Zaczynamy od rysunku

PIC

Rozpiszmy podaną informację o stosunku pola powierzchni bocznej do pola podstawy

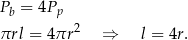
Pb = 4Pp 2 πrl = 4πr ⇒ l = 4r.

Teraz wykorzystajmy informację o obwodzie przekroju osiowego.

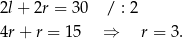
2l + 2r = 30 / : 2 4r + r = 15 ⇒ r = 3.

Zatem

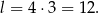
l = 4 ⋅3 = 12.

Z twierdzenia Pitagorasa obliczamy wysokość

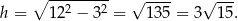
∘ --------- √ ---- √ --- h = 12 2 − 3 2 = 135 = 3 1 5.

Teraz już łatwo obliczyć objętość

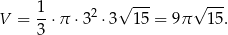
1 √ --- √ --- V = --⋅π ⋅ 32 ⋅3 15 = 9π 15. 3

 
Odpowiedź: √ --- V = 9π 15

Wersja PDF