Zadanie nr 9802980
Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 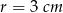 . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
. Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.
Rozwiązanie
Rozpoczynamy od rysunku – rysujemy przekrój osiowy opisanej sytuacji.
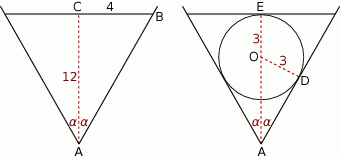
Sposób I
Ułóżmy najpierw plan działań. Jeżeli oznaczmy przez 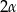 kąt rozwarcia stożka, to z podanych wysokości i promienia będziemy mogli wyliczyć funkcje trygonometryczne kąta
kąt rozwarcia stożka, to z podanych wysokości i promienia będziemy mogli wyliczyć funkcje trygonometryczne kąta  (lewy obrazek). To z kolei pozwoli obliczyć długość odcinka
(lewy obrazek). To z kolei pozwoli obliczyć długość odcinka 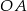 (prawy rysunek), a w konsekwencji też
(prawy rysunek), a w konsekwencji też 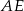 . Na koniec sprawdzimy, czy
. Na koniec sprawdzimy, czy 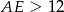 , czy też nie – od tego będzie zależała odpowiedź.
, czy też nie – od tego będzie zależała odpowiedź.
Liczymy. Z twierdzenia Pitagorasa w trójkącie 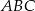 mamy
mamy
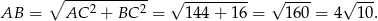
Zatem
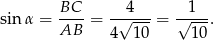
Teraz patrzymy na trójkąt 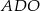 na prawym obrazku.
na prawym obrazku.
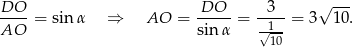
Zatem
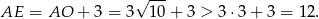
Zatem kulka będzie wystawać ze stożka.
Sposób II
Tym razem postąpimy inaczej: obliczmy promień kuli wpisanej w stożek o podanych wymiarach i sprawdzimy, czy promień ten jest większy, czy też mniejszy od 3 cm.
Patrzymy na trójkąt równoramienny otrzymany w przekroju stożka. Jego pole jest równe
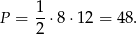
Korzystamy teraz ze wzoru na pole 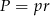 , gdzie
, gdzie 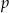 jest połową obwodu, a
jest połową obwodu, a  promieniem okręgu wpisanego.
promieniem okręgu wpisanego.
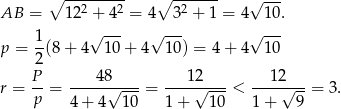
W takim razie kulka o promieniu 3 cm nie zmieści się w tym stożku.
Odpowiedź: Kulka będzie wystawać ponad brzeg naczynia.

