Zadanie nr 6058556
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 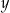 prawdziwa jest nierówność
prawdziwa jest nierówność
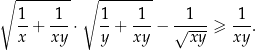
Rozwiązanie
Przekształcamy daną nierówność w sposób równoważny – korzystamy po drodze z faktu, że liczby  i
i 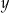 są dodatnie.
są dodatnie.
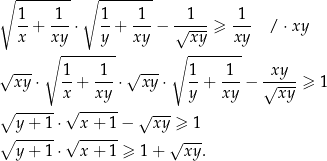
Obie strony są teraz nieujemne, więc możemy podnieść nierówność stronami do kwadratu.
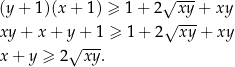
Sposób I
Podnosimy nierówność jeszcze raz stronami do kwadratu
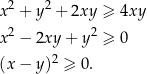
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy ją w sposób równoważny, więc wyjściowa nierówność też musiała być prawdziwa.
Sposób II
Nierówność możemy zapisać w postaci
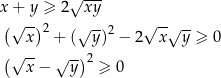
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy ją w sposób równoważny, więc wyjściowa nierówność też musiała być prawdziwa.

