/Konkursy/Zadania/Nierówności/3 liczby

Zadanie nr 7268198

Udowodnij, że dla dowolnych liczb 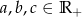a,b,c ∈ R + zachodzi nierówność

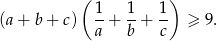
( 1 1 1) (a + b+ c) --+ -+ -- ≥ 9. a b c
Wersja PDF

Rozwiązanie

Wymnażając lewą stronę nierówności otrzymujemy

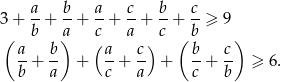
a b a c b c 3+ --+ --+ -+ --+ --+ --≥ 9 ( b a) (c a )c ( b ) a- b- a- c- b- c- b + a + c + a + c + b ≥ 6 .

Aby wykazać powyższą nierówność, wystarczy pokazać, że każdy z nawiasów jest 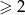≥ 2 . Sprawdźmy dla przykładu pierwszy nawias

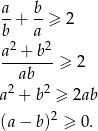
a b --+ --≥ 2 b 2 a2 a--+-b- ≥ 2 ab a2 + b2 ≥ 2ab (a − b)2 ≥ 0.

Otrzymana nierówność jest oczywiście prawdziwa. Podobnie sprawdzamy pozostałe dwa wyrażenia w nawiasach.

Wersja PDF