Zadanie nr 8915345
Udowodnić, że dla dowolnych nieujemnych liczb rzeczywistych 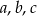 prawdziwa jest nierówność
prawdziwa jest nierówność
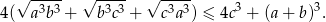
Rozwiązanie
Sposób I
Spróbujemy przkształcić podaną nierówność zwijając do pełnego kwadratu.
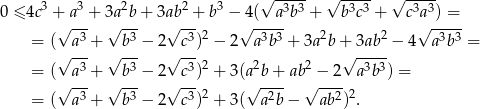
Jest jasne, że nierówność ta jest zawsze spełniona.
Sposób II
Ponieważ nierówność jest jednorodna (stopień każdego jednomianu to 3), więc łatwo możemy pozbyć się jednej niewiadomej, powiedzmy  , dzieląc przez
, dzieląc przez 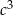 .
.
Osobno rozważmy najpierw przypadek 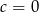 .
.
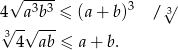
Nierówność ta łatwo wynika z nierówności między średnimi 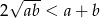 .
.
Jeżeli 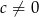 , to podzielmy obie strony przez
, to podzielmy obie strony przez 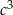 .
.
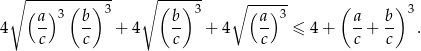
Podstawiamy teraz 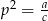 i
i 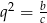 i mamy
i mamy