Zadanie nr 1368734
Rozwiąż nierówność 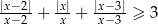 .
.
Rozwiązanie
Oczywiście musi być 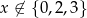 .
.
Sposób I
Aby opuścić wartości bezwględne rozważamy przypadki.
Jeżeli 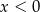 to mamy nierówność
to mamy nierówność
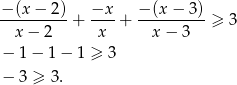
W tym przypadku nierówność jest więc sprzeczna.
Jeżeli 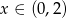 to mamy nierówność
to mamy nierówność
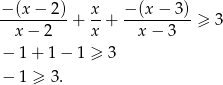
W tym przypadku nierówność jest więc sprzeczna.
Jeżeli 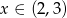 to mamy nierówność
to mamy nierówność
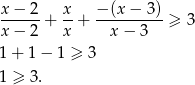
W tym przypadku nierówność jest więc sprzeczna.
Jeżeli 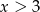 to mamy nierówność
to mamy nierówność
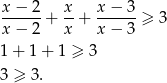
Nierówność jest więc spełniona dla dowolnego 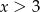 .
.
Sposób II
Zauważmy, że każde z wyrażeń 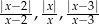 jest równe
jest równe 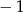 lub 1. Jeżeli więc suma tych wyrażeń ma być równa co najmniej 3, to każde z nich musi być równe 1. Tak będzie dokładnie wtedy, gdy każde z wyrażeń pod wartością bezwzględną będzie dodatnie, czyli dla
lub 1. Jeżeli więc suma tych wyrażeń ma być równa co najmniej 3, to każde z nich musi być równe 1. Tak będzie dokładnie wtedy, gdy każde z wyrażeń pod wartością bezwzględną będzie dodatnie, czyli dla 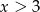 .
.
Odpowiedź: