/Szkoła średnia/Nierówności/Z wartością bezwzględną/Rozwiąż nierówność

Zadanie nr 1610210

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 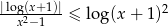|log(x+-1)| 2 x2− 1 ≤ log(x + 1 ) .

Rozwiązanie

Aby logarytm w nierówności miał sens, musi być

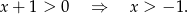
x + 1 > 0 ⇒ x > − 1.

Ponadto musi być 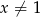x ⁄= 1 , ze względu na mianownik.

Chciałoby się opuścić wartość bezwględną, aby to jednak zrobić musimy wiedzieć jaki jest znak 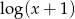log(x + 1) . Rozważmy dwa przypadki.

  • Jeżeli
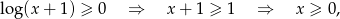
    log (x + 1) ≥ 0 ⇒ x + 1 ≥ 1 ⇒ x ≥ 0,

    to mamy nierówność

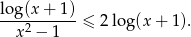
    lo g(x+ 1) -----------≤ 2 lo g(x + 1). x2 − 1

    Widać, że 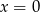x = 0 spełnia nierówność. Załóżmy zatem, że 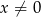x ⁄= 0 , wtedy logarytm jest dodatni i możemy przez niego podzielić.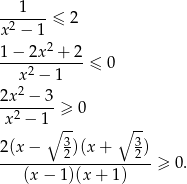

    1 -2-----≤ 2 x − 1 1−--2x2-+-2- x 2 − 1 ≤ 0 2 2x--−-3-≥ 0 x 2 − 1∘-- ∘ -- 3 3 2(x-−----2)(x+----2)- (x − 1)(x + 1) ≥ 0.

    Ponieważ 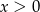x > 0 daje to nam nierówność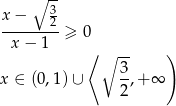

    ∘ -- x − 3 -------2 ≥ 0 x− 1 ⟨ ∘ -- ) x ∈ (0,1 )∪ 3,+ ∞ 2

    Zatem w tym przypadku mamy rozwiązanie

    ⟨ ∘ -- ) 3 ⟨0,1) ∪ --,+ ∞ . 2
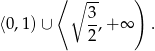
  • Jeżeli
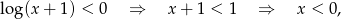
    log(x + 1 ) < 0 ⇒ x + 1 < 1 ⇒ x < 0,

    to mamy nierówność

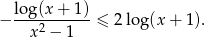
    log (x+ 1) − ---2-------≤ 2 lo g(x + 1). x − 1

    Ponieważ logarytm jest ujemny, możemy przez niego podzielić zmieniając znak nierówności.

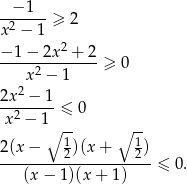
    − 1 -2-----≥ 2 x − 1 −-1−--2x2-+-2- x 2 − 1 ≥ 0 2 2x--−-1-≤ 0 x 2 − 1∘-- ∘ -- 1 1 2(x-−----2)(x+----2)- (x − 1)(x + 1) ≤ 0.

    Ponieważ 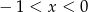− 1 < x < 0 , daje to nam nierówność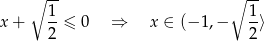

    ∘ -- ∘ -- 1 1 x + --≤ 0 ⇒ x ∈ (− 1,− --⟩ 2 2

 
Odpowiedź: ∘ -- ⟨ ∘ -- ) (− 1,− 12⟩∪ ⟨0,1) ∪ 32,+ ∞

Wersja PDF