/Szkoła średnia/Nierówności/Z wartością bezwzględną/Rozwiąż nierówność

Zadanie nr 3601409

Wyznacz największą liczbę całkowitą spełniającą nierówność 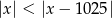|x | < |x − 1 025| .

Wersja PDF

Rozwiązanie

Sposób I

Rozpatrujemy 3 przypadki.

Jeżeli 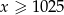x ≥ 1025 , to mamy nierówność

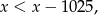
x < x− 1025,

która jest oczywiście sprzeczna.

Jeżeli 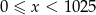0 ≤ x < 10 25 , to mamy nierówność

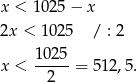
x < 1025 − x 2x < 102 5 / : 2 x < 10-25 = 51 2,5. 2

Trzeciego przypadku, czyli 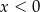x < 0 możemy nie sprawdzać, bo na pewno w tym przypadku nie otrzymamy większego rozwiązania.

Sposób II

Obie strony nierówności są nieujemne, więc możemy nierówność podnieść stronami do kwadratu.

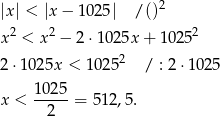
2 |x| < |x − 1025| / () x2 < x 2 − 2 ⋅1025x + 10252 2 2⋅ 1025x < 1025 / : 2⋅ 1025 1025 x < -----= 5 12,5. 2

Oczywiście największą liczbą całkowitą spełniającą tę nierówność jest 512.  
Odpowiedź: 512

Wersja PDF