Zadanie nr 4462784
Rozwiąż nierówność 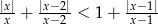 .
.
Rozwiązanie
Oczywiście musi być 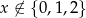 . Aby opuścić wartości bezwględne rozważamy przypadki.
. Aby opuścić wartości bezwględne rozważamy przypadki.
Jeżeli 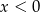 to mamy nierówność
to mamy nierówność
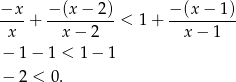
Nierówność jest więc spełniona dla dowolnego 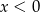 .
.
Jeżeli 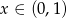 to mamy nierówność
to mamy nierówność
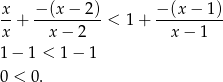
W tym przypadku nierówność jest więc sprzeczna.
Jeżeli 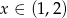 to mamy nierówność
to mamy nierówność
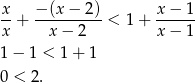
Nierówność jest więc spełniona dla dowolnego 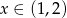 .
.
Jeżeli 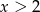 to mamy nierówność
to mamy nierówność
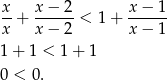
W tym przypadku nierówność jest więc sprzeczna.
Odpowiedź: