Zadanie nr 4602179
Rozwiąż nierówność 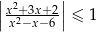 .
.
Rozwiązanie
Rozkładamy trójmian w liczniku.
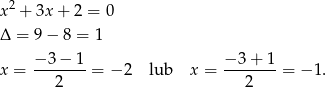
Teraz trójmian w mianowniku.
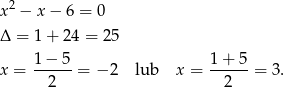
W takim razie dziedziną nierówności jest zbiór 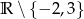 . Przy tym założeniu możemy nierówność przekształcić następująco.
. Przy tym założeniu możemy nierówność przekształcić następująco.
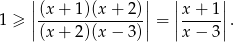
Dalsze przekształcenia wykonamy na dwa różne sposoby.
Sposób I
Przekształcamy nierówność.
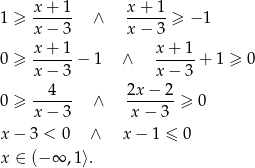
Uwzględniając dziedzinę nierówności, rozwiązaniem jest zbiór
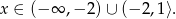
Sposób II
Mnożąc przez mianownik możemy nierówność zapisać w postaci
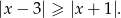
Obie strony są nieujemne, więc możemy nierówność podnieść stronami do kwadratu.
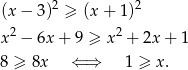
Uwzględniając dziedzinę nierówności, rozwiązaniem jest zbiór
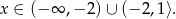
Odpowiedź: