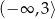/Szkoła średnia/Nierówności/Z wartością bezwzględną/Rozwiąż nierówność

Zadanie nr 4822344

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 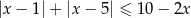|x − 1|+ |x − 5 | ≤ 1 0− 2x .

Rozwiązanie

Aby opuścić wartości bezwzględne musimy rozważyć trzy przypadki.

Jeżeli 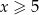x ≥ 5 to mamy nierówność

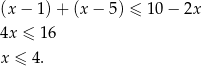
(x − 1) + (x − 5) ≤ 10 − 2x 4x ≤ 16 x ≤ 4 .

Ponieważ 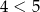4 < 5 , w tym przypadku zbiór rozwiązań jest pusty.

Jeżeli 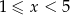1 ≤ x < 5 to mamy nierówność

x − 1 + (5 − x) ≤ 1 0− 2x 2x ≤ 6 ⇐ ⇒ x ≤ 3 ,

co w połączeniu z naszym założeniem daje przedział rozwiązań: 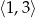⟨1 ,3⟩ .

Jeżeli 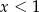x < 1 to mamy nierówność

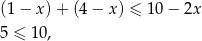
(1 − x) + (4 − x) ≤ 10 − 2x 5 ≤ 1 0,

która jest zawsze spełniona. W połączeniu z założeniem daje przedział rozwiązań 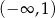(− ∞ ,1) .

Zatem rozwiązaniem nierówności jest zbiór

⟨1,3⟩ ∪ (− ∞ ,1) = (− ∞ ,3⟩.

 
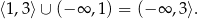
Odpowiedź: (− ∞ ,3⟩

Wersja PDF