Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 6827936

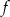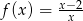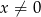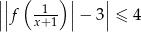Funkcja f jest określona wzorem x−-2 f (x) = x dla wszystkich liczb rzeczywistych x takich, że x ⁄= 0 . Rozwiąż nierówność || ( )| | ||||f -1--|| − 3|| ≤ 4 x+ 1 .

Wersja PDF
Rozwiązanie

Zauważmy, że

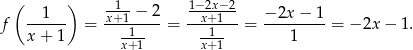
( ) -1-- 1−-2x−2 f --1--- = x+-1 −-2-= --x+1-- = −-2x−--1-= − 2x − 1 . x + 1 x1+-1 x1+1- 1

Musimy więc rozwiązać nierówność.

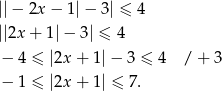
||− 2x − 1|− 3| ≤ 4 ||2x + 1| − 3| ≤ 4 − 4 ≤ |2x + 1|− 3 ≤ 4 / + 3 − 1 ≤ |2x + 1| ≤ 7.

Ponieważ wartość bezwzględna jest zawsze nieujemna, powyższa nierówność jest równoważna nierówności

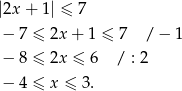
|2x + 1| ≤ 7 − 7 ≤ 2x + 1 ≤ 7 / − 1 − 8 ≤ 2x ≤ 6 / : 2 − 4 ≤ x ≤ 3.

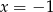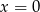Na koniec musimy pamiętać o usunięciu x = − 1 i x = 0 ze zbioru rozwiązań (ze względu na dziedzinę równania).  
Odpowiedź: x ∈ ⟨− 4,− 1) ∪ (− 1,0)∪ (0 ,3⟩

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!