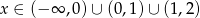Zadanie nr 7756497
Rozwiąż nierówność 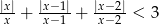 .
.
Rozwiązanie
Oczywiście musi być 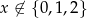 .
.
Sposób I
Aby opuścić wartości bezwględne rozważamy przypadki.
Jeżeli 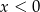 to mamy nierówność
to mamy nierówność
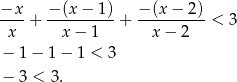
Nierówność jest więc spełniona dla każdego 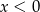 .
.
Jeżeli 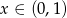 to mamy nierówność
to mamy nierówność
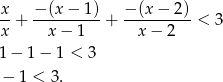
Nierówność jest więc też spełniona w przedziale 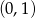 .
.
Jeżeli 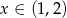 to mamy nierówność
to mamy nierówność
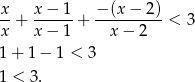
Nierówność jest więc też spełniona w przedziale 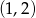 .
.
Jeżeli 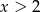 to mamy nierówność
to mamy nierówność
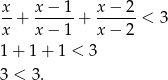
Nierówność jest więc w tym przypadku sprzeczna.
Sposób II
Zauważmy, że każde z wyrażeń 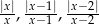 jest równe
jest równe 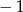 lub 1. W takim razie suma tych wyrażeń jest nie większa od 3 i jest równa 3 wtedy i tylko wtedy, gdy wszystkie wyrażenia pod wartościami bezwzględnymi są dodatnie, czyli dla
lub 1. W takim razie suma tych wyrażeń jest nie większa od 3 i jest równa 3 wtedy i tylko wtedy, gdy wszystkie wyrażenia pod wartościami bezwzględnymi są dodatnie, czyli dla 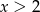 . W pozostałych przypadkach, czyli dla
. W pozostałych przypadkach, czyli dla 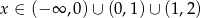 suma ta jest mniejsza od 3.
suma ta jest mniejsza od 3.
Odpowiedź: