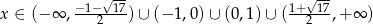/Szkoła średnia/Nierówności/Z wartością bezwzględną/Rozwiąż nierówność

Zadanie nr 8396483

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 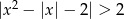2 |x − |x|− 2 | > 2 .

Rozwiązanie

Podana nierówność jest równoważna dwóm nierównościom

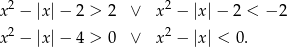
2 2 x − |x|− 2 > 2 ∨ x − |x |− 2 < −2 x 2 − |x|− 4 > 0 ∨ x2 − |x | < 0.

Jeżeli 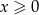x ≥ 0 to daje to nam nierówności

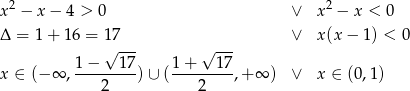
x2 − x − 4 > 0 ∨ x2 − x < 0 Δ = 1+ 16 = 1√7--- √ --- ∨ x(x − 1) < 0 1 − 17 1 + 1 7 x ∈ (− ∞ ,---------)∪ (---------,+ ∞ ) ∨ x ∈ (0 ,1 ) 2 2

Uwzględniając założenie 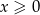x ≥ 0 daje to nam

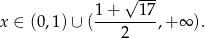
√ --- 1-+---17- x ∈ (0,1) ∪ ( 2 ,+∞ ).

Jeżeli natomiast 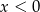x < 0 to mamy nierówności

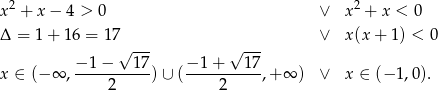
2 2 x + x − 4 > 0 ∨ x + x < 0 Δ = 1+ 16 = 17 ∨ x(x + 1 ) < 0 √ --- √ --- x ∈ (− ∞ , −-1-−--17-)∪ (−-1-+---17-,+ ∞ ) ∨ x ∈ (− 1,0). 2 2

Uwzględniając założenie 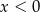x < 0 daje to nam

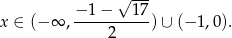
√ --- − 1 − 17 x ∈ (− ∞ ,-----------)∪ (− 1,0). 2

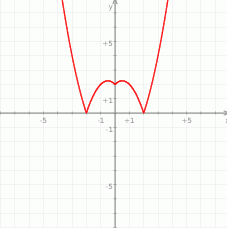
Na koniec, dla ciekawskich, wykres funkcji 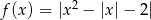f(x) = |x 2 − |x| − 2| .

PIC

 
Odpowiedź: √-- √-- x ∈ (− ∞ , −-1−2-17) ∪ (− 1,0)∪ (0,1)∪ ( 1+-217,+ ∞ )

Wersja PDF