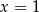Zadanie nr 8754047
Wyznacz najmniejszą liczbę całkowitą spełniającą nierówność
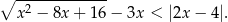
Rozwiązanie
Przekształćmy podaną nierówność
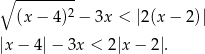
Musimy rozpatrzeć 3 przypadki
Jeżeli 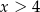 to mamy nierówność
to mamy nierówność
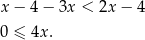
Zatem 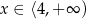 .
.
Jeżeli 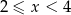 to mamy nierówność
to mamy nierówność
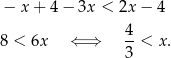
Zatem 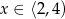 .
.
Jeżeli 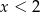 to mamy nierówność
to mamy nierówność
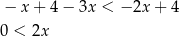
Zatem 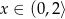 .
.
Łącząc wszystkie otrzymane odpowiedzi mamy: 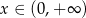 . W takim razie najmniejsza liczba całkowita spełniająca tę nierówność to
. W takim razie najmniejsza liczba całkowita spełniająca tę nierówność to 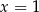 .
.
Odpowiedź: