Zadanie nr 9136110
Znajdź wszystkie liczby całkowite spełniające nierówność 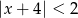 .
.
Rozwiązanie
Sposób I
Rozwiązaniem nierówności 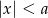 , gdzie
, gdzie 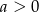 jest przedział
jest przedział 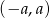 . W naszej sytuacji mamy więc
. W naszej sytuacji mamy więc
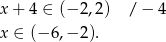
W przedziale tym znajdują się trzy liczby całkowite: 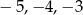 .
.
Sposób II
Nierówność 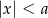 , gdzie
, gdzie 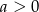 jest równoważna nierówności
jest równoważna nierówności 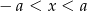 . W naszej sytuacji mamy więc
. W naszej sytuacji mamy więc
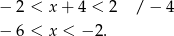
W przedziale tym znajdują się trzy liczby całkowite: 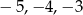 .
.
Sposób III
Jeżeli 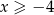 to wyrażenie pod wartością bezwzględną jest nieujemne i mamy nierówność
to wyrażenie pod wartością bezwzględną jest nieujemne i mamy nierówność
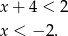
W tym przypadku mamy więc dwa rozwiązania całkowite: 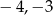 .
.
Jeżeli natomiast  to wyrażenie pod wartością bezwzględną jest ujemne i mamy nierówność
to wyrażenie pod wartością bezwzględną jest ujemne i mamy nierówność
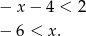
Tylko jedna liczba całkowita spełnia tę nierówność: 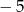 .
.
Sposób IV
Przypomnijmy, że nierówność
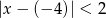
spełniają te liczby na osi liczbowej, które są odległe od 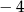 o mniej niż 2.
o mniej niż 2.

Jeżeli zaznaczymy ten zbiór na osi liczbowej, to widać, że zawiera on tylko trzy liczby całkowite 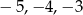 .
.
Odpowiedź: