Zadanie nr 9141727

Rozwiąż nierówność 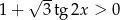√ -- 1 + 3 tg 2x > 0 w przedziale ⟨0,π ⟩ .

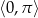Rozwiązanie

Ze względu na dziedzinę tangensa, musi być

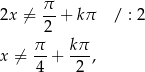
π 2x ⁄= 2-+ k π / : 2 x ⁄= π-+ kπ-, 4 2

co w danym przedziale oznacza, że

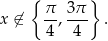
{ π 3π } x ⁄∈ --,--- . 4 4

Daną nierówność możemy zapisać w postaci

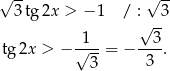
√ -- √ -- 3 tg2x > − 1 / : 3 1 √ 3- tg 2x > − √---= − ----. 3 3

Na razie nie zwracamy uwagi na to, że pod tangensem jest 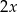i szkicujemy wykres tangensa.

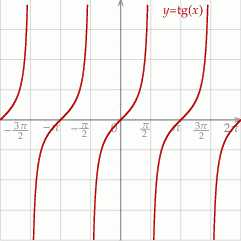
Z obrazka widać, że rozwiązaniem nierówności 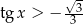√ - tgx > − -33 jest suma przedziałów postaci

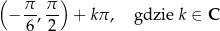
( π π ) − --,-- + k π, gdzie k ∈ C 6 2

My jednak mamy rozwiązać nierówność 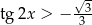√-3 tg 2x > − 3 , czyli

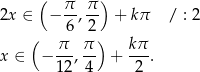
( π π ) 2x ∈ − 6-,2- + kπ / : 2 ( ) x ∈ − π-, π- + kπ-. 12 4 2

Pozostało teraz zauważyć, że część wspólna tych przedziałów i przedziału 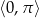⟨0,π ⟩ to zbiór

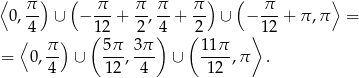
⟨ π ) ( π π π π ) ( π ⟩ 0,-- ∪ − ---+ --,--+ -- ∪ − ---+ π,π = ⟨4 ) 1( 2 2 4) (2 ⟩1 2 π- 5π- 3π- 11π- = 0,4 ∪ 12 , 4 ∪ 12 ,π .

Odpowiedź: ( ⟩ ⟨ π) (5π- 3π) 11π x ∈ 0 ,4 ∪ 12 ,4 ∪ 12 ,π