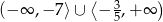Zadanie nr 9619170

Rozwiąż nierówność 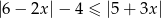|6 − 2x|− 4 ≤ |5+ 3x| .

Rozwiązanie

Zapiszmy podaną nierówność w postaci

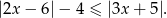
|2x − 6| − 4 ≤ |3x + 5|.

Wyrażenie pod pierwszą wartością bezwzględną zeruje się dla 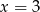x = 3 , a wyrażenie pod drugą dla 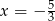x = − 53 , więc mamy do rozpatrzenia 3 przypadki.

Jeżeli 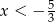x < − 5 3 to wyrażenia pod obydwiema wartościami bezwzględnymi są ujemne i mamy nierówność

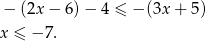
− (2x− 6)− 4 ≤ − (3x + 5) x ≤ − 7.

Czyli w tym przypadku otrzymujemy przedział: 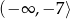(−∞ ,− 7⟩ .

Jeżeli 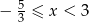− 5≤ x < 3 3 to mamy nierówność

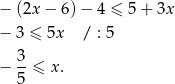
− (2x − 6)− 4 ≤ 5+ 3x − 3 ≤ 5x / : 5 3- − 5 ≤ x.

W tym przypadku otrzymujemy więc przedział rozwiązań: 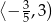⟨ ) − 35,3 .

Jeżeli wreszcie 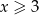x ≥ 3 to wyrażenia pod obydwiema wartościami bezwzględnymi są dodatnie i mamy nierówność

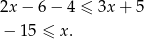
2x − 6 − 4 ≤ 3x + 5 − 15 ≤ x .

W tym przypadku otrzymujemy więc zbiór rozwiązań: 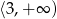⟨3,+ ∞ ) .

Rozwiązaniem nierówności jest więc

⟨ ) 3- (− ∞ ,− 7⟩ ∪ − 5,+ ∞ .

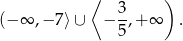
Odpowiedź: ⟨ 3 ) (− ∞ ,− 7⟩ ∪ − 5,+ ∞