Zadanie nr 7918773
Wyznacz wszystkie wartości parametru 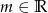 , dla których zbiór rozwiązań nierówności
, dla których zbiór rozwiązań nierówności
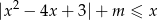
jest jednoelementowy.
Rozwiązanie
Sposób I
Sprawdzimy jaki jest znak wyrażenia pod wartością bezwzględną, co pozwoli nam się jej pozbyć. Liczymy pierwiastki trójmianu.
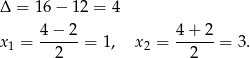
Aby opuścić wartość bezwzględną musimy rozważyć dwa przypadki.
- Jeżeli
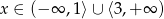 , to mamy nierówność
, to mamy nierówność 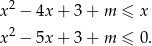
Musimy się teraz zastanowić kiedy ta nierówność ma dokładnie jedno rozwiązanie. Nie jest to całkiem proste, bo mamy ograniczenie
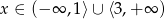 , więc można sobie wyobrazić, że nawet jak lewa strona ma dwa pierwiastki, to nierówność może mieć tylko jedno rozwiązanie.
, więc można sobie wyobrazić, że nawet jak lewa strona ma dwa pierwiastki, to nierówność może mieć tylko jedno rozwiązanie. Gdyby pierwiastek był w zbiorze
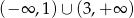 to w jego pobliżu lewa strona byłaby zarówno dodatnia jak i ujemna, co dawałoby nieskończenie wiele rozwiązań tej nierówności (szkicujemy sobie obrazek!). Zatem jedynym rozwiązaniem tej nierówności musi być liczba
to w jego pobliżu lewa strona byłaby zarówno dodatnia jak i ujemna, co dawałoby nieskończenie wiele rozwiązań tej nierówności (szkicujemy sobie obrazek!). Zatem jedynym rozwiązaniem tej nierówności musi być liczba 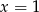 lub
lub 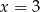 . Daje nam to odpowiednio
. Daje nam to odpowiednio 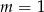 i
i 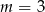 . Mamy zatem nierówności
. Mamy zatem nierówności 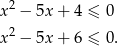
Łatwo sprawdzić, że rozwiązaniem pierwszej jest przedział
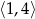 , a drugiej
, a drugiej 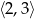 . Uwzględniając obowiązujący nas przedział
. Uwzględniając obowiązujący nas przedział 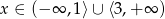 , widzimy, że tylko druga z nich spełnia żądany warunek.
, widzimy, że tylko druga z nich spełnia żądany warunek. Inny sposób sprawdzenia kiedy nierówność
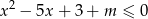
ma dokładnie jedno rozwiązanie, to zauważenie, że prosta
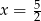 jest osią symetrii paraboli będącej wykresem lewej strony (przechodzi przez jej wierzchołek).
jest osią symetrii paraboli będącej wykresem lewej strony (przechodzi przez jej wierzchołek). 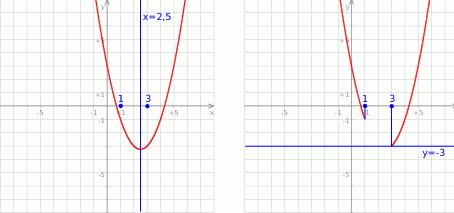
Ponieważ od
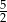 jest bliżej do 3 niż do 1, więc jeżeli ta parabola ma pierwiastek w przedziale
jest bliżej do 3 niż do 1, więc jeżeli ta parabola ma pierwiastek w przedziale 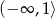 to ma też w przedziale
to ma też w przedziale 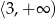 . Jeżeli pierwiastek ma być jeden, to musi być on w przedziale
. Jeżeli pierwiastek ma być jeden, to musi być on w przedziale 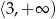 . Jak poprzednio zauważamy, że musi to być koniec przedziału, co daje nam
. Jak poprzednio zauważamy, że musi to być koniec przedziału, co daje nam 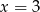 i
i 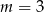 .
. Jeszcze inny sposób, to zapisanie nierówności w postaci
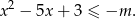
Teraz szkicujemy parabolę będącą wykresem lewej strony i zauważamy, że jej najmniejsza wartość na interesującym nas przedziale to
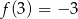 . Zatem powyższa nierówność będzie miała dokładnie jedno rozwiązanie tylko dla
. Zatem powyższa nierówność będzie miała dokładnie jedno rozwiązanie tylko dla 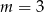 .
. - Jeżeli natomiast
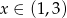 to mamy nierówność
to mamy nierówność 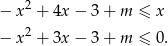
Jeżeli nierówność ta ma przynajmniej jedno rozwiązanie, to z założenia jest ono w przedziale otwartym
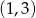 , więc jest wtedy nieskończenie wiele rozwiązań (bo w pobliżu pierwiastka parabola jest zarówno dodatnia jak i ujemna). To oznacza, że to jedyne rozwiązanie nierówności musi jednak być w przedziale
, więc jest wtedy nieskończenie wiele rozwiązań (bo w pobliżu pierwiastka parabola jest zarówno dodatnia jak i ujemna). To oznacza, że to jedyne rozwiązanie nierówności musi jednak być w przedziale 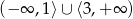 i wracamy do analizy z poprzedniego podpunktu.
i wracamy do analizy z poprzedniego podpunktu.
Sposób II
Zadanie można łatwo rozwiązać geometrycznie. Zacznijmy od naszkicowania wykresu funkcji 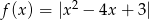 . Jak zauważyliśmy w poprzednim rozwiązaniu pierwiastkami paraboli pod wartością bezwzględną są liczby
. Jak zauważyliśmy w poprzednim rozwiązaniu pierwiastkami paraboli pod wartością bezwzględną są liczby 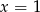 i
i 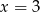 . Wykres
. Wykres 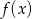 powstaje więc z paraboli
powstaje więc z paraboli 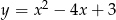 przez odbicie jej fragmentu na przedziale
przez odbicie jej fragmentu na przedziale 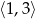 względem osi
względem osi 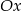 .
.
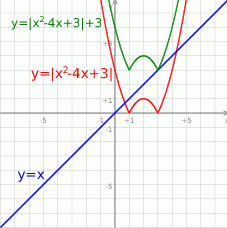
Pytanie teraz brzmi o ile trzeba tę parabolę przesunąć w górę lub w dół (odpowiada to dodawaniu 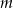 ), aby była poniżej wykresu
), aby była poniżej wykresu 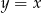 dokładnie w jednym punkcie. Gdy naszkicujemy sobie tę sytuację, to widać, że tak będzie jeżeli wartość przesuniętej funkcji w
dokładnie w jednym punkcie. Gdy naszkicujemy sobie tę sytuację, to widać, że tak będzie jeżeli wartość przesuniętej funkcji w 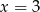 będzie równa 3 (czyli punkt ten będzie na prostej
będzie równa 3 (czyli punkt ten będzie na prostej 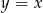 ). To nam daje
). To nam daje 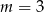 .
.
Odpowiedź: