Zadanie nr 3726257
Naszkicuj wykres funkcji 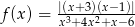 .
.
Rozwiązanie
Rozłóżmy najpierw wyrażenie z mianownika. W tym celu wstawiamy do wielomianu dzielniki wyrazu wolnego, czyli liczby -1,1,-2,2,-3,3,-6,6, tak długo aż dla jakiejś wyjdzie 0 – wychodzi już dla 1 . Jak już mamy pierwiastek, to dzielimy wielomian przez (x-1) . Robimy to tak jak umiemy, schemat Hornera, dzielenie wielomianów lub grupowanie odpowiednich czynników. My zrobimy to tą ostatnią metodą.
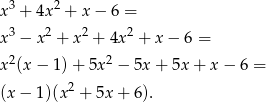
Rozwiązujemy równanie kwadratowe w nawiasie, 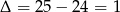 ,
, 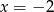 lub
lub 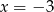 . Mamy zatem
. Mamy zatem
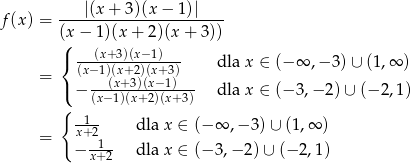
Wykres funkcji 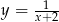 to hiperbola przesunięta o dwie jednostki w lewo. W przypadku naszej funkcji, na przedziałach
to hiperbola przesunięta o dwie jednostki w lewo. W przypadku naszej funkcji, na przedziałach 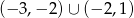 musimy odbić ten wykres względem osi
musimy odbić ten wykres względem osi  . Możemy w takim razie naszkicować wykres (na rysunku są narysowane zarówno funkcja
. Możemy w takim razie naszkicować wykres (na rysunku są narysowane zarówno funkcja 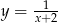 jak i
jak i 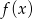 ).
).