/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z kwadratową

Zadanie nr 3948501

Dodaj do ulubionych
Dodaj do rozwiązanych

Naszkicuj wykres funkcji 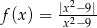|x2−-9| f (x) = x2− 9 . Określ dziedzinę oraz zbiór wartości funkcji.

Rozwiązanie

Zauważmy, że

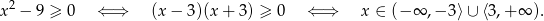
2 x − 9 ≥ 0 ⇐ ⇒ (x − 3)(x + 3 ) ≥ 0 ⇐ ⇒ x ∈ (− ∞ ,− 3⟩ ∪ ⟨3,+ ∞ ).

Ponadto zera mianownika, czyli liczby -3 i 3 nie należą do dziedziny, czyli

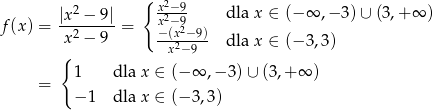
2 { x2−-9 dla x ∈ (− ∞ ,− 3)∪ (3 ,+∞ ) f (x) = |x--−-9| = x2− 92 x2 − 9 −(x2-−9) dla x ∈ (− 3,3) { x −9 1 dla x ∈ (−∞ ,− 3) ∪ (3,+ ∞ ) = − 1 dla x ∈ (−3 ,3)

Teraz bez trudu szkicujemy wykres.

PIC

 
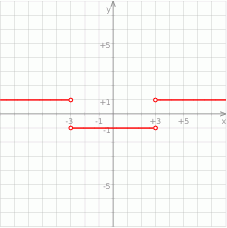
Odpowiedź: Dziedzina: 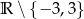R ∖ {− 3,3} , zbiór wartości: {− 1,1 }

Wersja PDF