/Szkoła średnia/Zadania z treścią/Liczba osób

Zadanie nr 5828971

Dodaj do ulubionych
Dodaj do rozwiązanych

Grupa znajomych postanowiła raz w tygodniu wynajmować salę gimnastyczną. Jednorazowa opłata za wynajęcie sali wynosiła 240 zł i podzielono ją na równe części tak, aby każdy ze znajomych płacił tyle samo. W drugim tygodniu do grupy dołączyły jeszcze dwie osoby i wówczas opłata przypadająca na każdego ze znajomych zmniejszyła się o 4 złote. Ile osób liczyła ta grupa w pierwszym tygodniu użytkowania sali?

Rozwiązanie

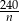Jeżeli oznaczymy liczbę znajomych przez n , to początkowo każda z osób miała płacić 24n0 złotych. Po dołączeniu dwóch osób opłata zmniejszyła się o 4 złote i jednocześnie wynosiła 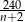240- n+2 . Mamy więc równanie

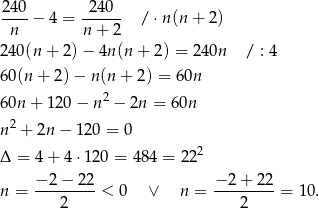
2-40 -24-0- n − 4 = n + 2 / ⋅n (n+ 2) 240 (n+ 2)− 4n(n + 2) = 2 40n / : 4 60(n + 2)− n (n + 2) = 60n 2 60n + 120− n − 2n = 60n n2 + 2n − 1 20 = 0 2 Δ = 4 + 4⋅ 120 = 484 = 22 − 2− 22 − 2 + 22 n = ---------< 0 ∨ n = ---------= 10. 2 2

Ujemne rozwiązanie odrzucamy i mamy 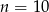n = 10 .  
Odpowiedź: 10 osób

Wersja PDF