Zadanie nr 6065545
Dobierz wartości 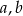 i
i  tak, aby liczby
tak, aby liczby 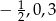 były pierwiastkami wielomianu
były pierwiastkami wielomianu 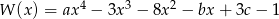 .
.
Rozwiązanie
Najłatwiej jest z 0 jako pierwiastkiem. Mamy mieć
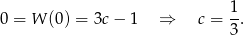
Podstawiając tę wartość zostaje nam wielomian
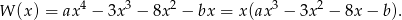
Na tego  -a przed nawiasem możemy nie zwracać uwagi, bo na pewno się nie zeruje ani dla
-a przed nawiasem możemy nie zwracać uwagi, bo na pewno się nie zeruje ani dla 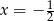 , ani dla
, ani dla 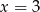 . Zatem zerować się musi wyrażenie w nawiasie, co prowadzi do układu równań
. Zatem zerować się musi wyrażenie w nawiasie, co prowadzi do układu równań
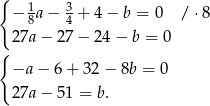
Wstawiamy teraz 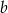 z drugiego równania do pierwszego
z drugiego równania do pierwszego
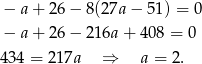
Zatem 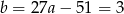 .
.
Odpowiedź: