Zadanie nr 6951058
Wyznacz wszystkie wartości parametru 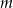 , dla których równanie
, dla których równanie 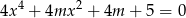 ma cztery różne pierwiastki rzeczywiste spełniające warunek
ma cztery różne pierwiastki rzeczywiste spełniające warunek
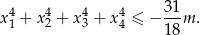
Rozwiązanie
Mamy do czynienia z równaniem dwukwadratowym więc podstawiamy 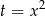 .
.
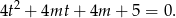
Aby dane równanie 4-tego stopnia miało cztery pierwiastki powyższe równanie musi mieć dwa różne pierwiastki dodatnie (bo 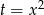 ). Na początek sprawdźmy kiedy równanie kwadratowe ma dwa pierwiastki.
). Na początek sprawdźmy kiedy równanie kwadratowe ma dwa pierwiastki.
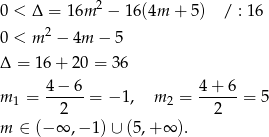
Teraz trzeba jeszcze sprawdzić, kiedy pierwiastki te są dodatnie. Na mocy wzorów Viète’a tak będzie, gdy
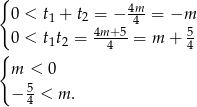
W połączeniu z warunkiem na 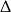 -ę daje to
-ę daje to 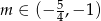 .
.
Jeżeli 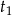 i
i 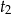 są pierwiastkami równania kwadratowego, to pierwiastki oryginalnego równania są równe
są pierwiastkami równania kwadratowego, to pierwiastki oryginalnego równania są równe 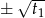 i
i 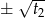 . Zatem
. Zatem
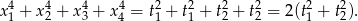
Na mocy wzorów Viète’a suma ta jest równa
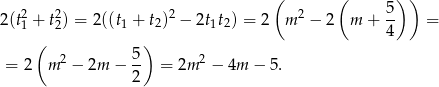
Otrzymujemy stąd nierówność
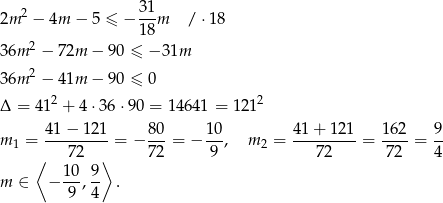
Ponieważ
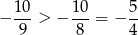
w połączeniu z wcześniejszą nierównością na 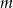 mamy
mamy
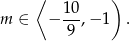
Odpowiedź: