Zadanie nr 7345229
Rozwiąż równanie 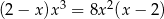 .
.
Rozwiązanie
Sposób I
Przekształcamy równanie.
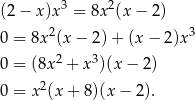
Równanie ma więc trzy rozwiązania: 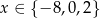 .
.
Sposób II
Gołym okiem widać dwa pierwiastki równania: 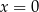 i
i 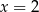 (bo dla
(bo dla 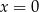 i
i 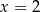 obie strony równania są równe 0). Jeżeli natomiast
obie strony równania są równe 0). Jeżeli natomiast 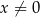 i
i 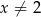 to możemy obie strony podzielić przez
to możemy obie strony podzielić przez 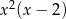 .
.
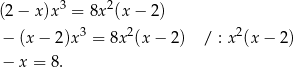
Trzecim pierwiastkiem równania jest więc 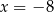 .
.
Sposób III
Przekształcamy równanie.
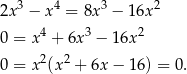
Jednym z pierwiastków jest więc 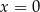 . Aby wyznaczyć pozostałe rozwiązujemy równanie kwadratowe
. Aby wyznaczyć pozostałe rozwiązujemy równanie kwadratowe
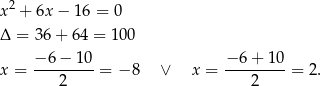
Odpowiedź: