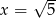/Szkoła średnia/Równania/Wielomianowe/Stopnia 4

Zadanie nr 9931496

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 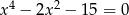4 2 x − 2x − 15 = 0 .

Rozwiązanie

Sposób I

Jest to równanie dwukwadratowe, więc podstawiamy 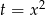2 t = x i mamy równanie

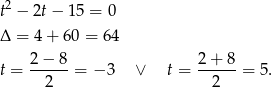
2 t − 2t− 15 = 0 Δ = 4 + 60 = 6 4 2− 8 2 + 8 t = -----= − 3 ∨ t = ------= 5. 2 2

Ponieważ 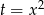2 t = x , ujemne rozwiązanie odrzucamy i dostajemy

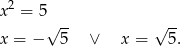
x2 = 5 √ -- √ -- x = − 5 ∨ x = 5.

Sposób II

Przekształćmy dane równanie korzystając z obserwacji: 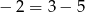− 2 = 3− 5 .

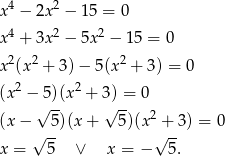
4 2 x − 2x − 15 = 0 x4 + 3x2 − 5x2 − 15 = 0 2 2 2 x (x + 3)− 5(x + 3) = 0 (x2 − 5)(x2 + 3) = 0 √ -- √ -- (x− 5)(x+ 5)(x2 + 3) = 0 √ -- √ -- x = 5 ∨ x = − 5.

 
Odpowiedź: 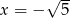√ -- x = − 5 lub √ -- x = 5

Wersja PDF