/Szkoła średnia/Nierówności/Kwadratowe/Z parametrem

Zadanie nr 3350935

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest nierówność kwadratowa z parametrem 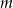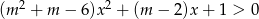m : 2 2 (m + m − 6)x + (m − 2 )x+ 1 > 0 . Dla jakich wartości parametru 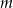m nierówność jest spełniona przez każdą liczbę rzeczywistą?

Rozwiązanie

Sprawdźmy najpierw kiedy lewa strona nierówności jest liniowa, czyli kiedy współczynnik przy 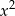x2 jest zerowy.

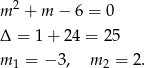
2 m + m − 6 = 0 Δ = 1+ 24 = 25 m 1 = − 3, m 2 = 2.

Dla 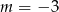m = − 3 mamy nierówność 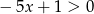− 5x + 1 > 0 , która nie jest zawsze spełniona, natomiast dla 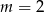m = 2 mamy nierówność 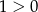1 > 0 i jest OK.

Zastanówmy się teraz nad przypadkiem, gdy lewa strona jest kwadratowa. Aby cała parabola będąca jej wykresem była powyżej osi 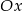Ox , jej ramiona muszą być skierowane do góry oraz musi być Δ < 0 .

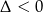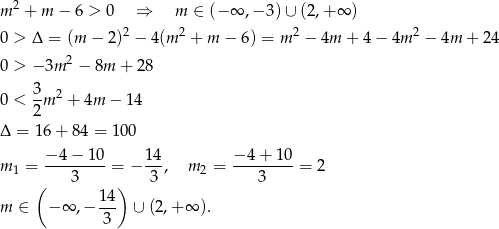
2 m + m − 6 > 0 ⇒ m ∈ (− ∞ ,− 3) ∪ (2,+ ∞ ) 0 > Δ = (m − 2)2 − 4 (m2 + m − 6) = m 2 − 4m + 4 − 4m 2 − 4m + 24 2 0 > − 3m − 8m + 28 3 2 0 < --m + 4m − 14 2 Δ = 16+ 84 = 100 − 4− 10 14 − 4+ 1 0 m 1 = ---3-----= − 3-, m 2 = ---3-----= 2 ( ) m ∈ − ∞ ,− 14- ∪ (2,+ ∞ ). 3

Łącząc wszystkie otrzymane warunki, mamy

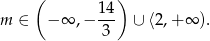
( 14 ) m ∈ − ∞ ,− --- ∪ ⟨2,+ ∞ ). 3

 
Odpowiedź: ( ) m ∈ − ∞ ,− 143 ∪ ⟨2,+ ∞ )

Wersja PDF