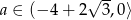/Szkoła średnia/Nierówności/Kwadratowe/Z parametrem

Zadanie nr 5613663

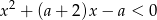Dla jakich wartości parametru a zbiór rozwiązań nierówności x 2 + (a + 2)x − a < 0 jest niepusty i należą do niego tylko liczby ujemne?

Wersja PDF

Rozwiązanie

Aby podana nierówność miała niepusty zbiór rozwiązań musimy mieć 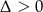Δ > 0 , czyli

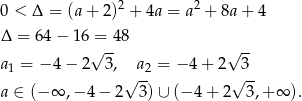
2 2 0 < Δ = (a + 2 ) + 4a = a + 8a+ 4 Δ = 64 − 16 = 48 √ -- √ -- a 1 = − 4− 2 3, a2 = − 4 + 2 3 √ -- √ -- a ∈ (− ∞ ,− 4 − 2 3) ∪ (− 4+ 2 3,+ ∞ ).

Sposób I

Wykresem lewej strony nierówności jest parabola, więc tak należy sobie myśleć o postawionym problemie: jaki warunek musi być spełniony aby parabola o ramionach skierowanych w górę i przecinająca oś 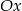Ox była powyżej osi 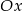Ox (może też ją dotykać) dla 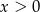x > 0 ? Aby tak było jej wierzchołek musi być na lewo od 0 oraz w 0 musi mieć nieujemną wartość.

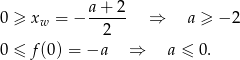
a+--2- 0 ≥ xw = − 2 ⇒ a ≥ − 2 0 ≤ f(0) = −a ⇒ a ≤ 0.

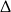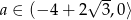W połączeniu z nierównością na Δ -ę mamy więc √ -- a ∈ (− 4+ 2 3,0⟩ .

Sposób II

Ponieważ wykresem funkcji 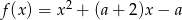2 f(x) = x + (a+ 2)x− a jest parabola o ramionach skierowanych w górę, warunek zadania będzie spełniony jeżeli większy z pierwiastków 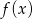f(x) będzie niedodatni. Musimy więc rozwiązać nierówność

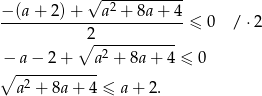
√ ------------ −-(a-+-2)-+---a2 +-8a+--4 2 ≤ 0 / ⋅2 ∘ -2---------- −∘ -a−--2+----a + 8a+ 4 ≤ 0 a2 + 8a + 4 ≤ a + 2 .

Jeżeli prawa strona jest ujemna, czyli 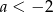a < − 2 to nierówność jest sprzeczna. Musi więc być 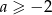a ≥ − 2 i przy tym założeniu możemy nierówność podnieść stronami do kwadratu.

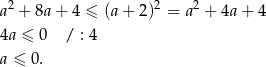
2 2 2 a + 8a+ 4 ≤ (a+ 2) = a + 4a + 4 4a ≤ 0 / : 4 a ≤ 0.

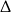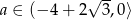W połączeniu z nierównością na Δ -ę mamy więc √ -- a ∈ (− 4+ 2 3,0⟩ .

Sposób III

Tak jak w poprzednim sposobie zauważamy, że większy z pierwiastków lewej strony musi być niedodatni. Zauważmy, że warunek ten możemy zapisać przy pomocy wzorów Viète’a.

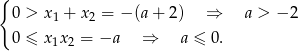
{ 0 > x1 + x2 = − (a+ 2) ⇒ a > − 2 0 ≤ x1x2 = −a ⇒ a ≤ 0.

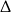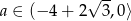W połączeniu z warunkiem na Δ -ę otrzymujemy więc √ -- a ∈ (− 4+ 2 3,0⟩ .  
Odpowiedź: √ -- a ∈ (− 4 + 2 3,0 ⟩

Wersja PDF