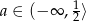Zadanie nr 7379946
Dla jakich wartości parametru  zbiór rozwiązań nierówności
zbiór rozwiązań nierówności 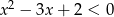 jest zawarty w zbiorze rozwiązań nierówności
jest zawarty w zbiorze rozwiązań nierówności 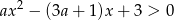 ?
?
Rozwiązanie
Zacznijmy od rozwiązania pierwszej nierówności.
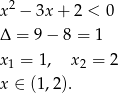
Musimy więc ustalić kiedy parabola 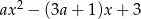 jest powyżej osi
jest powyżej osi 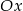 na przedziale
na przedziale 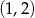 .
.
Jeżeli 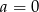 to mamy nierówność
to mamy nierówność 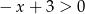 , której zbiór rozwiązań zawiera przedział
, której zbiór rozwiązań zawiera przedział 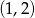 .
.
Jeżeli 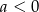 , to ramiona paraboli
, to ramiona paraboli 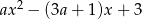 są skierowane w dół i wystarczy aby jej wartości były nieujemne w końcach przedziału
są skierowane w dół i wystarczy aby jej wartości były nieujemne w końcach przedziału 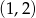 .
.
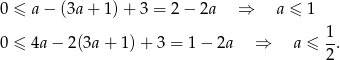
Mamy więc w tym przypadku  .
.
Jeżeli  , to ramiona paraboli
, to ramiona paraboli 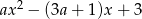 są skierowane do góry. Kiedy będzie ona powyżej osi na przedziale
są skierowane do góry. Kiedy będzie ona powyżej osi na przedziale 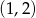 ? – jest kilka możliwości. Sprawdźmy kiedy cała parabola jest powyżej osi (
? – jest kilka możliwości. Sprawdźmy kiedy cała parabola jest powyżej osi (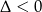 ).
).
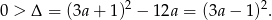
Nierówność ta jest oczywiście sprzeczna.
Ponieważ parabola zawsze przecina oś 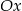 , jej wierzchołek musi być poza przedziałem
, jej wierzchołek musi być poza przedziałem 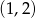 , a wartości w końcach przedziału muszą być nieujemne. Wartości na końcach przedziału już sprawdzaliśmy – są nieujemne dla
, a wartości w końcach przedziału muszą być nieujemne. Wartości na końcach przedziału już sprawdzaliśmy – są nieujemne dla 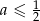 , pozostaje więc sprawdzić warunek z wierzchołkiem.
, pozostaje więc sprawdzić warunek z wierzchołkiem.
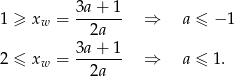
Mamy zatem w tym przypadku 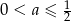 .
.
Uwzględniając wszystkie rozpatrzone przypadki mamy 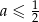
Odpowiedź: