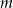/Szkoła średnia/Nierówności/Kwadratowe/Z parametrem

Zadanie nr 7852115

Dla jakich wartości parametru 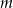m nierówność 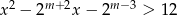2 m+ 2 m− 3 x − 2 x− 2 > 12 jest prawdziwa dla każdej liczby rzeczywistej.

Wersja PDF

Rozwiązanie

Sposób I

Mamy nierówność kwadratową

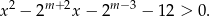
x2 − 2m+ 2x − 2m−3 − 12 > 0.

Ponieważ wykresem lewej strony jest parabola o ramionach skierowanych do góry, nierówność ta będzie zawsze spełniona jeżeli 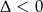Δ < 0 , czyli gdy wykres nie przecina osi Ox .

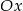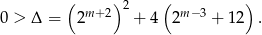
( m+2) 2 ( m− 3 ) 0 > Δ = 2 + 4 2 + 12 .

Widać, że prawa strona jest dodatnia, więc nie ma takiej wartości 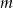m .

Sposób II

Zauważmy, że dla dowolnego 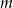m , wstawiając 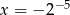−5 x = −2 otrzymujemy nierówność

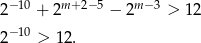
− 10 m+2− 5 m−3 2 + 2 − 2 > 1 2 2− 10 > 12.

Nierówność jest fałszywa, więc nie ma takiego 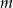m .  
Odpowiedź: Nie ma takiego m

Wersja PDF