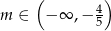/Szkoła średnia/Nierówności/Kwadratowe/Z parametrem

Zadanie nr 8623973

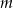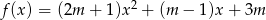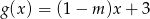Dla jakich wartości parametru m wartości funkcji 2 f(x) = (2m + 1)x + (m − 1)x + 3m są dla każdego argumentu x mniejsze od odpowiednich wartości funkcji g (x ) = (1− m )x+ 3 ?

Wersja PDF

Rozwiązanie

Musimy sprawdzić kiedy rozwiązaniem nierówności

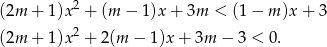
2 (2m + 1)x + (m − 1)x + 3m < (1 − m )x + 3 (2m + 1)x 2 + 2 (m − 1)x + 3m − 3 < 0.

jest zbiór liczb rzeczywistych. Jeżeli lewa strona jest liniowa, czyli dla 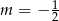1 m = − 2 , mamy nierówność, która nie jest zawsze spełniona.

Jeżeli wykres lewej strony jest parabolą, to jej ramiona muszą być skierowane w dół (czyli 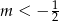m < − 12 ) oraz musi być Δ < 0 .

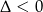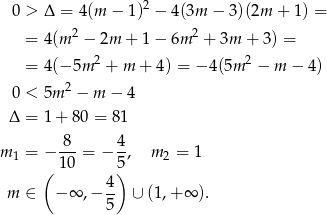
2 0 > Δ = 4(m − 1) − 4(3m − 3)(2m + 1) = = 4(m2 − 2m + 1 − 6m 2 + 3m + 3 ) = = 4(− 5m 2 + m + 4) = − 4(5m 2 − m − 4) 2 0 < 5m − m − 4 Δ = 1+ 8 0 = 81 m1 = − 8--= − 4-, m 2 = 1 ( 10 5) 4- m ∈ − ∞ ,− 5 ∪ (1,+ ∞ ).

Musimy jeszcze uwzględnić założenie 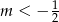m < − 1 2 , więc odpowiedzią jest przedział ( ) m ∈ −∞ ,− 45 .  
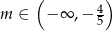Odpowiedź: ( ) m ∈ − ∞ ,− 45

Wersja PDF