Zadanie nr 8690233

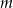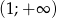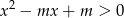Znajdź wszystkie wartości parametru , dla których zbiór (1;+ ∞ ) zawiera się w zbiorze rozwiązań nierówności x2 − mx + m > 0 .

Wersja PDF

Rozwiązanie

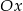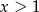Jak zwykle myślimy o praboli – pytanie brzmi kiedy parabola o ramionach skierowanych w górę jest powyżej osi dla x > 1 ? Możliwe są dwie sytuacje.

Pierwsza możliwość, to że cała parabola jest powyżej osi .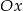

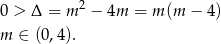
0 > Δ = m 2 − 4m = m(m − 4) m ∈ (0 ,4).

Jeżeli natomiast parabola przecina oś 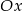, to jej wierzchołek musi być na lewo od 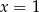x = 1 i wartość w 1 musi być nieujemna.

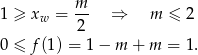
1 ≥ xw = m- ⇒ m ≤ 2 2 0 ≤ f(1) = 1 − m + m = 1.

Odpowiedź: m ∈ (− ∞ ,4)

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz