/Szkoła średnia/Nierówności/Kwadratowe/Z parametrem

Zadanie nr 9635461

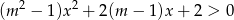Wyznacz wszystkie wartości x , dla których nierówność (m 2 − 1)x2 + 2(m − 1)x + 2 > 0 jest prawdziwa dla każdego m ∈ R .

Wersja PDF

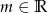Rozwiązanie

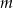Zadanie jest podchwytliwe (złośliwe), bo zamieniona jest rola x -a i m -a. Przekształćmy je najpierw, grupując względem potęg m .

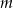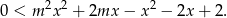
0 < m 2x2 + 2mx − x2 − 2x+ 2.

Jeżeli 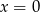x = 0 , to mamy nierówność 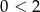0 < 2 , która jest zawsze spełniona.

Możemy zatem założyć, że wykresem prawej strony jest parabola o ramionach skierowanych w górę. Aby była ona powyżej osi musi być spełniony warunek 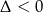Δ < 0 , czyli

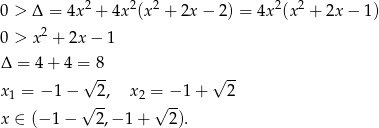
0 > Δ = 4x 2 + 4x 2(x2 + 2x − 2) = 4x 2(x2 + 2x− 1) 0 > x 2 + 2x − 1 Δ = 4+ 4 = 8 √ -- √ -- x1 = − 1 − 2, x2 = − 1 + 2 √ -- √ -- x ∈ (− 1 − 2,− 1 + 2).

Oczywiście w powyższych rachunkach korzystaliśmy już z faktu, że 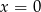x = 0 jest OK.  
Odpowiedź: √ -- √ -- x ∈ (− 1 − 2,− 1 + 2)

Wersja PDF